
1. introduction
the plane geometry diagram parsing dataset (pgdp5k) was constructed by the 澳门游戏娱乐场棋牌 (nlpr), (casia). our dataset consists of 5000 diagram samples composed of 16 shapes, covering 5 positional relations, 22 symbol types and 6 text types, labeled with more fine-grained annotations at primitive level, including primitive classes, locations and relationships, where 1,813 non-duplicated images are selected from the and other 3,187 images are collected from three popular textbooks across grades 6-12 on by taking screenshots from pdf books. combined with above annotations and geometric prior knowledge, it can generate intelligible geometric propositions automatically and uniquely.
download: (80.7 mb)
2. annotations
2.1. geometric primitives
we divided geometric primitives into 3 classes: point, line and circle,
and we annotated their parsing positions and uniform pixel widths.
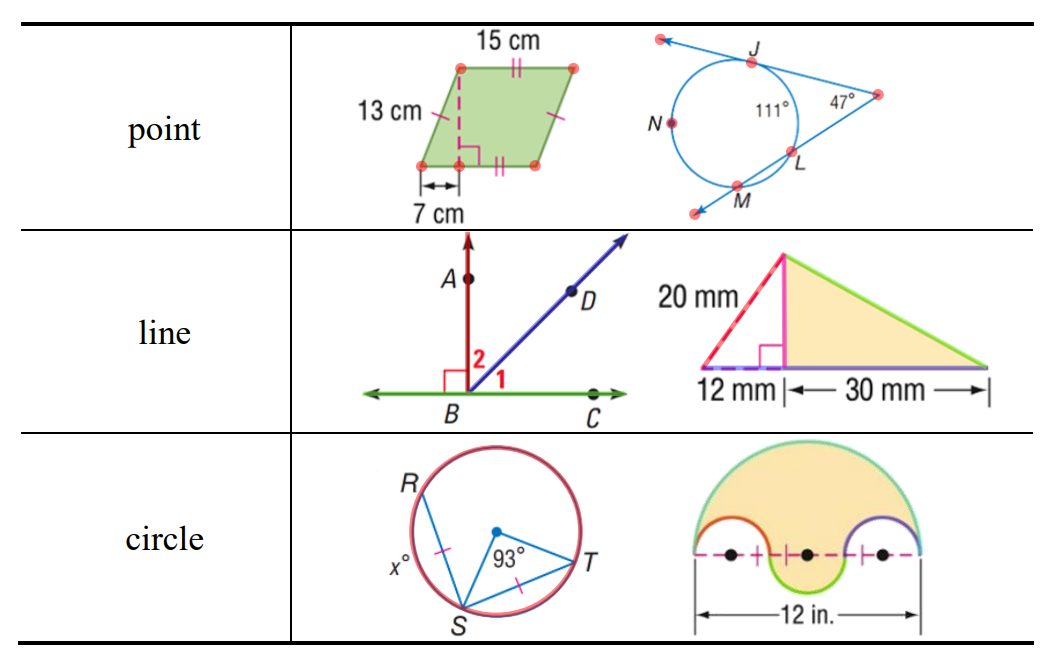
fig. 1 examples of geometric primitive.
2.2. non-geometric primitives
for non-geometric primitives, we annotated the bounding box, symbol class and text class, and
recorded corresponding text contents.
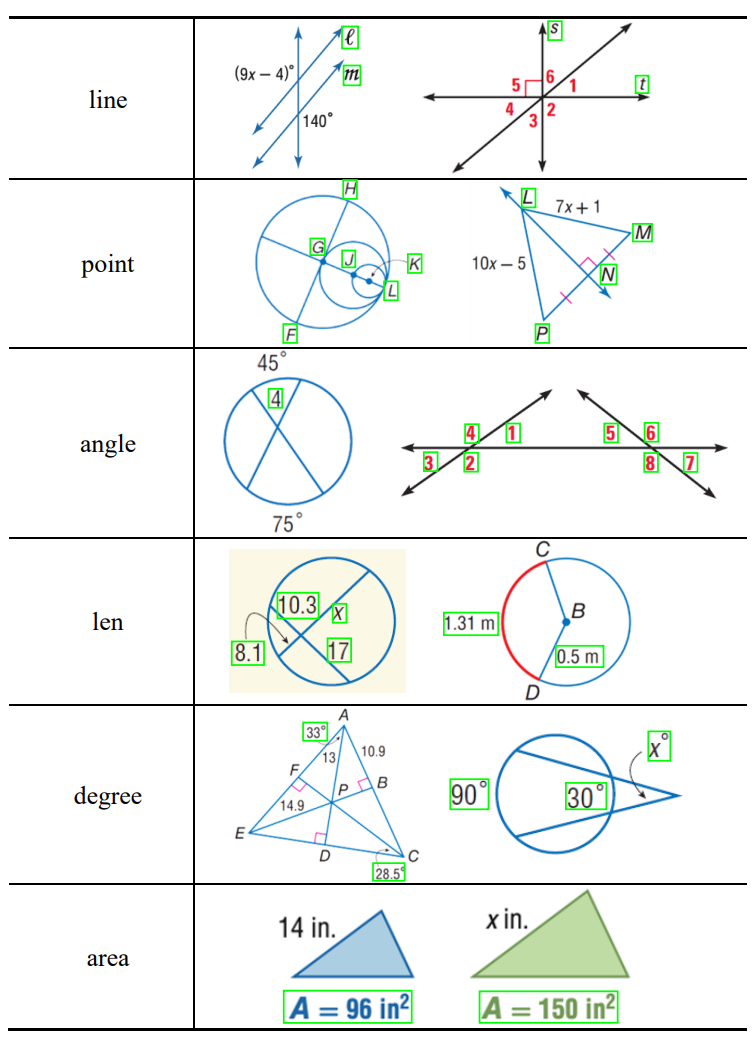
fig. 2 examples of text.
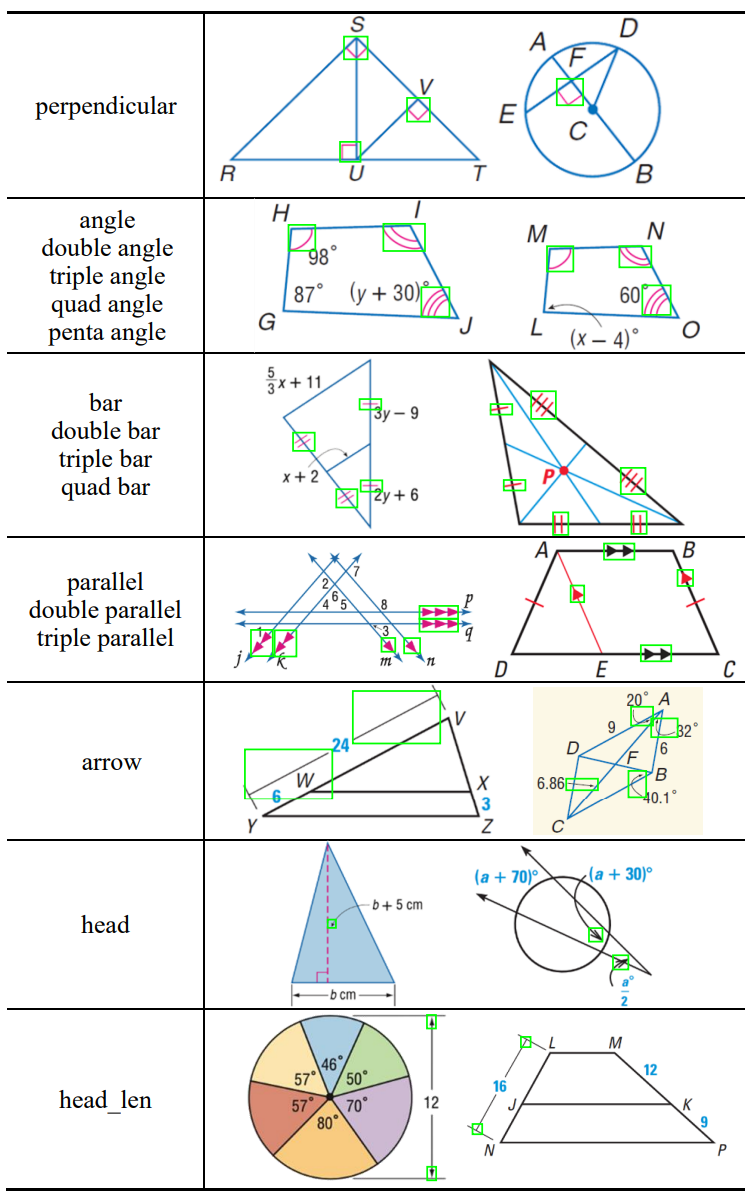
fig. 3 examples of symbol.
2.3. relationships
as to primitive relations, we constructed a relation graph of elementary relations among primitives in fig. 4. we divided primitive relations into 4 classes: geo2geo, text2geo, sym2geo and sym2text. for relations of geometric primitives, we only construct relations between point and line, point and circle, because other high-level relations among geometric primitives could be derived from these two basic relations. we defined a two-tuple with multiple entities to represent the relation between primitives. we take points, symbols and texts as subjects, and set other primitives related as objects. some relation tuples are shown in fig. 5.
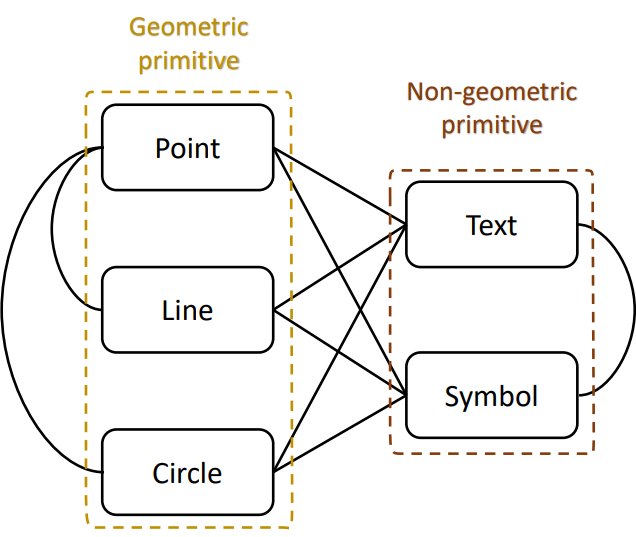
fig. 4 primitive relationship graph of plane geometry diagram.
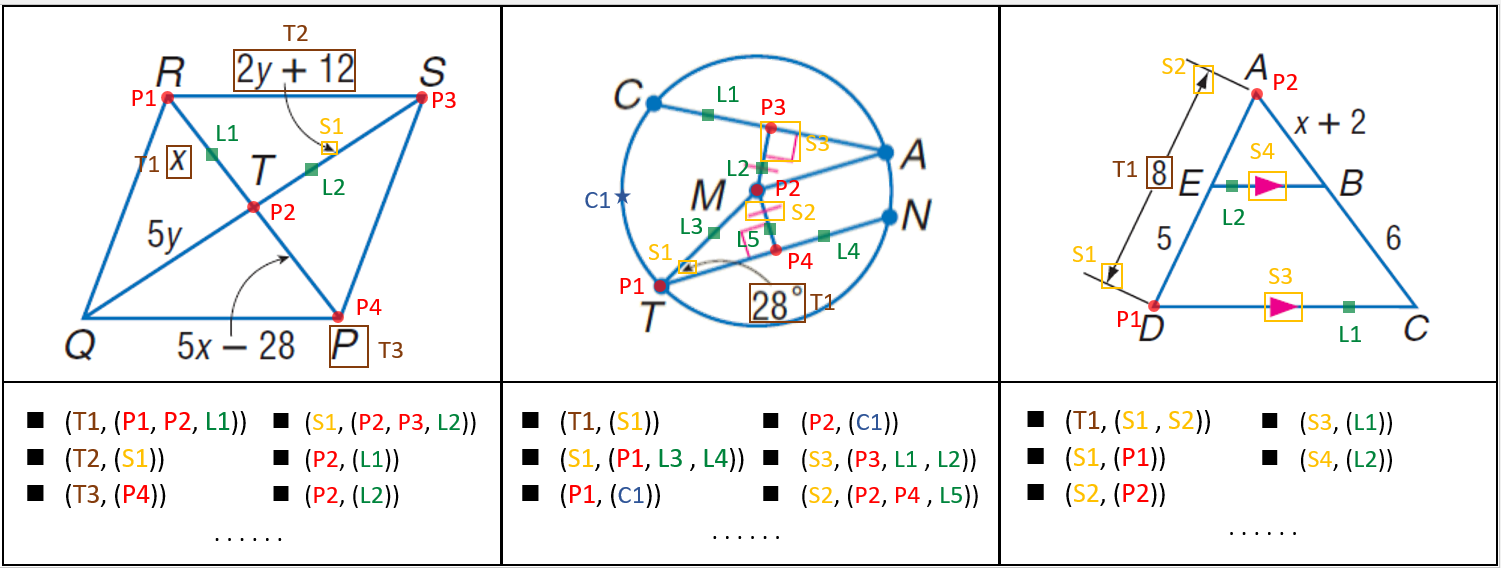
fig. 5 relation tuples of pgdp5k dataset. 'p#', 'l#', 'c#', 't#'' and 's#'' denote instances of point, line, circle, text and symbol, respectively.
2.4. geometric description language
we formed the high-level and comprehensible specifications of geometric description
language (gdl), which mainly consists of a list of geometric propositions formatted by
proposition templates. as shown in tab. 1, we defined 4 types of proposition templates
about basic relations: geometry shape, geo2geo, text2geo and sym2geo.
table. 1 geometric proposition templates of primitive relation. '$' represents geometric primitives and '&' denotes text content.
|
relation class |
primitive class |
proposition templates |
|
geo shape |
point |
· point($) |
|
line |
· line($,$), line($) |
|
|
circle |
· circle($,radius_$) |
|
|
angle |
· angle($,$,$), angle($) |
|
|
arc |
· arc($,$), arc($,$,$) |
|
|
geo2geo |
point |
· pointliesonline($,line($,$)) · pointliesoncircle($,circle($,radius_$)) · circle($,radius_$) |
|
text(&)2geo |
text_point |
·point(&) |
|
text_line |
·line(&) |
|
|
text_angle |
·equals(measureof(angle($,$,$)),mea-sureof(angle &)) |
|
|
text_degree |
·equals(measureof(angle($,$,$)), &) ·equals(measureof(arc($,$)), &) |
|
|
text_length |
·equals(lengthof(line($,$)), &) ·equals(lengthof(arc($,$)), &) |
|
|
text_area |
- |
|
|
sym2geo |
sym_perpendicular |
· perpendicular(line($,$), line($,$)) |
|
sym_angle |
·equals(measureof(angle($,$,$)), measureof(angle($,$,$))) |
|
|
sym_bar |
·equals(lengthof(line($,$)), lengthof(line($,$))) ·equals(lengthof(arc($,$)), lengthof(arc($,$))) |
|
|
sym_parallel |
·parallel(line($,$), line($,$)) |
2.5. dataset distributions
fig. 6 displays class distributions of geometry shape, symbol, text and relation. they are all subject to the long-tailed distribution evidently. note that text is seen as a special symbol recorded in the symbol distribution.
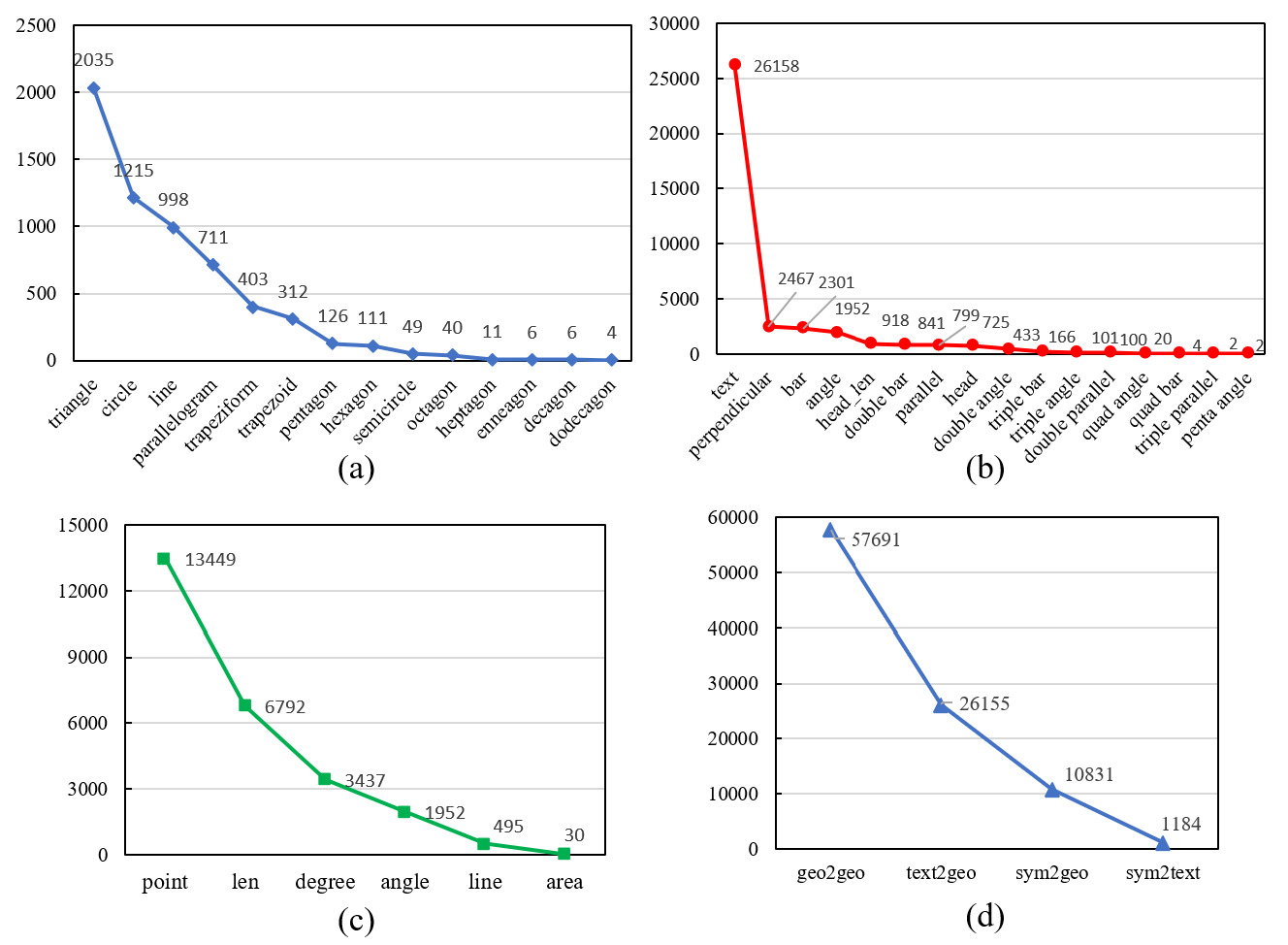
fig. 6 distributions of pgdp5k dataset. (a)(b)(c)(d) denote the class distribution of shape, symbol, text and relation, respectively.
2.6. dataset formats

fig. 7 format of annotation

fig. 8 format of logic form
3. condition of use
reference
a comprehensive description of pgdp5k dataset was described in:
the dataset was firstly used in the research work:
if this dataset helps you, please cite the papers above.
contact
fei yin (fyin@nlpr.ia.ac.cn)
national laboratory of pattern recognition (nlpr)
institute of automation of chinese academy of sciences
95 zhongguancun east road, beijing 100190, p.r. china
haidian | beijing | china
phone : ( 86-10)8254-4797
fax : ( 86-10) 8254-4594
email:liucl@nlpr.ia.ac.cn
website:www.nlpr.ia.ac.cn/pal/